Manacher's Algorithm（求最长回文子串）

本文讲述 Manacher 算法（马拉车算法）的原理以及如何利用 Manacher 算法获取最长回文子串。

给定一个字符串s，找到这个字符串的最长回文子串

Example 1:

1 2 3

Input: "babad" Output: "bab" Note: "aba" is also a valid answer.

Example 2:

1 2	Input: "cbbd" Output: "bb"

要找到一个字符串中的最长回文子串有以下几种方法：

1. 暴力搜索，算法复杂度O(N³)
2. 动态规划，算法复杂度O(N²)
3. Manacher算法，算法复杂度O(N)

而本文的主角就是Manacher’s algorithm，一起来看看它的实现

核心思想

Manacher算法的核心思想在于搜索以每个字符为中心的回文子串长度，并利用先前搜索的结果加快后续回文子串长度的计算

其中从中心向两边搜索是Manacher和动态规划方法相比暴力搜索降低复杂度的关键，而利用先前的搜索结果加快后续回文子串计算则是Manacher算法能够以不可思议的O(N)复杂度完成回文串查找的关键

过程

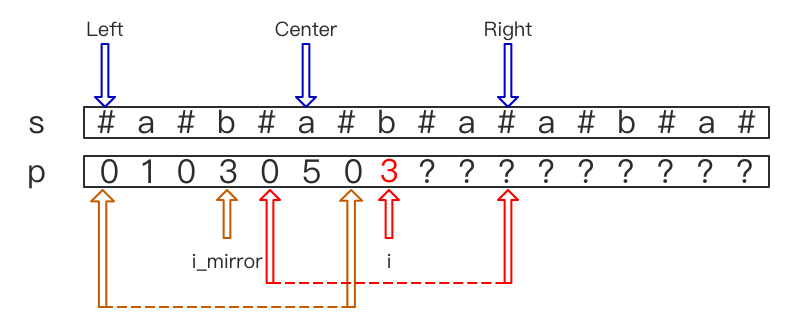
以Manacher算法的一个中间过程为例

s：给定的字符串

P：手动维护，P[i]保存以i位置为中心的最长子串长度

Center：当前最近的回文子串中心

Left：最近回文子串的左边界

RIght：最近回文子串的右边界

i：当前位置

要计算i位置的回文子串长度P[i]，根据Manacher算法的核心思想，我们需要以i为中心，向两边扩张计算回文子串的长度，而在这之前，我们可以通过一些方式获得P[i]的最小值以减少计算量，一共有以下两种情况：

1. 当前位置i位于右边界R之前
2. 当前位置i位于右边界R之后

首先讨论第一种i < R的情况，也就是如上图所示的情况

在这种情况下，由于i在以Center为中心的回文子串内，因此我们可以通过下图中与i相对的i_mirror来加速对P[i]的运算

i_mirror = 2 * Center - i

由于串C是回文的，因此以i为中心的回文子串最少应该与以i_mirror为中心的回文子串长度相当（中心对称），如下图：


此时P[i] = P[i_mirror]

那么这是唯一的情况么，答案是否定的，在上图中由于串i_mirror完全包含在串C当中，因此我们可以认为串i与串i_mirror是中心对称的，可以复用其长度，然而若回文串i_mirror与串C只有部分重合呢？考虑如下图所示的情况

在对给定的字符串做了一些小小的改动后（如绿色字体所示），我们得到了一组新的回文串C，此时我们可以看到，位置i相对于Center的镜像位置i_mirror，其最长回文串不是包含在串C中的（仅有部分重叠），那么这种情况下P[i]的值又该是多少呢?

答案是R-i

这里实际上借助了中心对称的特性，使用R-i计算串i_mirror与串C重叠的部分

因此综合之前的情况，在第一种情况下，P[i]的最小值为

min(R-i, P[i_mirror])

其中i_mirror = 2 * C - i

接下来讨论第二种情况，当i > R时，P[i]的值应该是多少

答案应该是显而易见的，当i > R时，我们没有任何可以参考的信息（这和计算P[0]的情况是相当的），因此这时P[i] = 0，我们需要从0开始逐步向两边扩张

综合上述两种情况，我们就得到了任意位置的P[i]初始值为

R > i ? min( R-i, P[i_mirror]) : 0

在获得了初始值之后，我们就可以以此为起点，不断向两边扩张了，以代码形式我们的行为是这样的：

1
2
3
4
5

//直到以i为中心的s[left] != s[right]为止
while( s[ i-1-P[i] ] == s[ i+1+P[i] ]) {
  	//回文串i扩张
    P[i] ++;
}

在这之后若新的回文串i的右边界超过了原先串C的右边界，那么我们需要更新串C为当前的串i，原因是计算后续位置的回文串时在串C内的部分至少在串i内也是回文的

按照此步骤不断进行，最后我们就可以得到一个填充完毕的P[i]如下：

其中最大值6就是我们想要得到的最长回文子串长度，返回该部分子串即可

References

Manacher’s Algorithm

最长回文子串——Manacher 算法